剑指Offer-2

-- 本章重点导航 -- Day1 JZ51 JZ56

Day 1

JZ38：排列组合@next_permutation

排列组合如何通过代码实现？

• 手撕next_permtation

标准的“下一个排列”算法可以描述为：

1. 在尽可能靠右的低位进行交换，需要从后向前查找

2. 将一个 尽可能小的「大数」 与前面的「小数」交换，将「大数」换到前面。「大数」后面的所有数需置为升序，升序排列就是最小的排列。

图示

public String[] permutation(String s) {
	List<String> res = new ArrayList<String>();
	char[] arr = s.toCharArray();
	Arrays.sort(arr);//优先得到第一个排列
	do {
		res.add(new String(arr));
	} while (next_permutation(arr));
	int size = ret.size();
	String[] ans = new String[size];
	for (int i = 0; i < size; i++) {
		ans[i] = ret.get(i);
	}
	return ans;
}
public boolean next_permutation(char[] nums) {
	int len = nums.length;
	for (int i = len - 1; i > 0; i--) {
		if (nums[i] > nums[i - 1]) {//首先找到首个相邻递增对
			Arrays.sort(nums, i, len);//直接升序
			for (int j = i; j < len; j++) {//交换[i-1]与第一个大者
				if (nums[j] > nums[i - 1]) {
					char temp = nums[j];
					nums[j] = nums[i - 1];
					nums[i - 1] = temp;
					return true;
				}
			}
		}
	}
	//Arrays.sort(nums);//用于321->123
	return false;

而组合，也可以用递归考虑。

JZ39：数组中频率超过一半的数字@快速排序与中位数

参考：dsacpp-12.2.2

记“过半数元素”为众数。设P为向量A中长度为2m的前缀。若元素x在P中恰好出现m次，仅当后缀A-P拥有众数，A有众数，且A-P的众数就是A的众数。若A的众数就是x，则在剪除前缀P之后，x与非众数均减少相同的数目，二者数目的差距在后缀A-P中保持不变。反过来，若A的众数为y，则在剪除前缀P之后，y减少的数目也不致多于非众数减少的数目，二者数目的差距在后缀A-P中也不会缩小。

template <typename T> T majEleCandidate(Vector<T>A){
	T maj;//众数候选者，始终为当前前缀中出现次数不少于一半的某个元素
    //线性扫描：借助计数器c,记录maj与其它元素的数目差
	for(int c=0,i=0; i<A.size(); i++)
		if(0==c){//每当c归零，都意味着此时的前缀P可以剪除
			maj=A[i];c=1;//众数候选者改为新的当前元素
		}else//否则
			maj==A[i]?c++:c--;//相应地更新差额计数器
		return maj;//至此，原向量的众数若存在，则只能是maj——尽管反之不然
}

上面的方法很难想到，但是基于快速排序的partition选取方便想到，在此介绍：

本题其实是选中间位置。

template <typename T> void quickSelect ( Vector<T> &A, Rank k ){
	for(Rank lo=0, hi=A.size()-1; lo < hi; ){
		Rank i = lo, j = hi; T pivot = A[lo];
		while(i<j){//注意顺序,先j--
			while ( (i < j)&&(pivot<=A[j]) ) j--;     
			A[i] = A[j];
			while ( (i < j)&&(A[i]<=pivot) ) i++;     
			A[j] = A[i];
		}//assert:i==j.得到pivot所应该在是下标
		A[i]=pivot;
        if ( k <= i ) hi = i - 1;//只查左段
	    if ( i <= k ) lo = i + 1;//只查右段
    }
}

JZ40：数组中最小的k个数

参考上面的快速partition选取，取A[0..k)即可。

=>拓展：如果需要去掉重复元素？P1138 第 k 小整数 - 洛谷

TopK专题

参：dsacpp12.2.6

本节将延续以上快速选取算法的思路，介绍一个在最坏情况下运行时间依然为O(n)的k-选取算法。

0)if(n=|A|<Q)return trivialselect(A,k);//递归基：序列规模不大时直接使用蛮力算法
1)将A均匀地划分为n/Q个子序列，各含Q个元素；//Q为一个不大的常数，如：5
2)各子序列分别排序，计算中位数，并将这些中位数组成一个序列；//可采用任何排序算法，比如选择排序
3)通过递归调用本函数select(),计算出中位数序列的中位数，记作M;
4)根据其相对于M的大小，将A中元素分为三个子集：L(小于）、E(相等）和G(大于）;
5)  if (|L| > k) return select(L, k);
	else if (|L| + |E| ≥ k) return M;	
	else return select ( G , k - | L | - | E | ) ;

image-20220215003301907

上述算法从理论上证实，的确可以在线性时间内完成k-选取。然而很遗憾，其线性复杂度中的常系数项过大，以致在通常规模的应用中难以真正体现出效率的优势。

下面介绍一种更适合处理海量数据、无需修改数组本身的堆局部排序算法，时间复杂度是O(nlogn)。

Java 中提供了现成的 PriorityQueue（默认小根堆），可以直接地处理TopK大问题。重写构造器，

PriorityQueue< >((x, y) -> (y - x)) 可方便实现大根堆。

 public int[] getLeastK(int[] arr, int k) {
        Queue<Integer> pq = new PriorityQueue<>((x, y) -> y - x);
        for (int num: arr) {
            if (pq.size() < k) {
                pq.offer(num);
            } else if (num < pq.peek()) {//peek为顶端->根->最大
                pq.poll(); pq.offer(num);
            }
        }
        int[] res = new int[k];
        int idx = 0;
        for(int num: pq) {
            res[idx++] = num;
        }
        return res;
    }

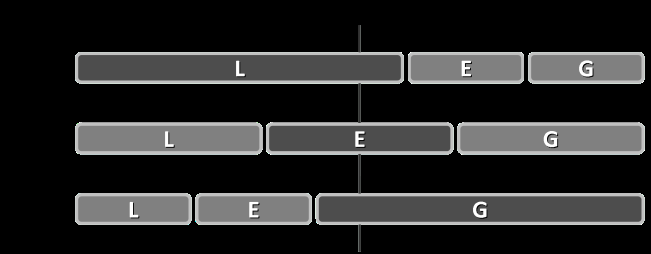
Day2

JZ41：数据流的中位数@就地堆选取

妙啊，开两个堆。我们把数组存储成[小大根堆|大小根堆]。

class MedianFinder {
        private PriorityQueue<Integer> lpq,rpq;
        public MedianFinder() {
            lpq = new PriorityQueue<Integer>((x,y)->y-x);
            rpq = new PriorityQueue<Integer>();
        }
        public void addNum(int num) {//妙操作：轮换加最值，达到分类效果。
            if(lpq.size() == rpq.size()){//原有偶数，加到rpq
                lpq.offer(num);//更新并获得根
                rpq.offer(lpq.poll());
            } else {//否则加到lpq，保持平衡
                rpq.offer(num);
                lpq.offer(rpq.poll());
            }
        }
        public double findMedian() {
            if(lpq.size() == rpq.size()){
                return ( lpq.peek() + rpq.peek() ) / 2.0;
            } else {
                return rpq.peek();
            }
        }
    }

JZ43：求1~N中数字1出现的次数

用递归的思维，去找规律。同样适用于以下题目，精妙略。

		if ( n < 10 )    return 1;
        int lenpow = 1, res = 0;//拆分n == [high|cur(1bit)|low]
        int high = n / 10, cur = n % 10, low = 0;
        while(high != 0 || cur != 0) {//说明n已经全在low部分，即被处理过
            if(cur == 0) res += high * lenpow;
            else if(cur == 1) res += high * lenpow + low + 1;
            else res += (high + 1) * lenpow;//这是发现的规律
            low += cur * lenpow;
            lenpow *= 10;
            cur = high % 10;
            high /= 10;
        }
        return res;

参考：数位 DP - OI Wiki (oi-wiki.org)

• JZ44：数字序列中某一位的数字

      int findNthDigit(int n) {
          long cnt = 1;
          int len = 1;
          if(n <= 1) return n;
          while(cnt <= n){
              cnt += len * 9 * pow(10, len - 1);
              len++;
          }
          len--;
          int toEnd = ceil( (cnt - 1.0 *n)/len );
          cout << toEnd;
          return ((int)pow(10,len) - toEnd) / (int)pow(10, (cnt-n-1)%len) % 10;
      }

• JZ45：数组重排粘贴成最小的数

• JZ46：数字翻译成字符串

  由小到大分析->动态规划

Day3

JZ47：数组中最大和路径@滚动dp

我们发现状态转移的方向不同行且不同列，显然互不干扰，于是：

		for(int i = 0; i < m; ++i){
            dp[0] += grid[i][0];//记得设置初始转移状态
            for (int j = 1; j < n; j++) {
                dp[j] = Math.max(dp[j-1], dp[j]) + grid[i][j];
            }
        }
        return dp[n-1];

JZ48：最长不含重复字符的子字符串@滑动窗口

滑动窗口实际上就是双指针，维护一个具有特定性质的“窗口”。

		Map<Character, Integer> dic = new HashMap<>();
        int i = -1, res = 0;//注意双指针的初始含义，使左指针作开区间
        for(int j = 0; j < s.length(); j++) {
            if(dic.containsKey(s.charAt(j)))//维护性质：无重复字符
                i = Math.max(i, dic.get(s.charAt(j))); 
            dic.put(s.charAt(j), j); // dic记录字符位置
            res = Math.max(res, j - i); //维护性质：最长
        }
        return res;

JZ49：丑数@指针就地dp

本题涵盖两种思想。

• 动态规划的最优子结构思想。

• 通过指针存储状态，便于比大小的思想。

JZ50： 字符串首个只出现一次的字符@有序哈希

Java 使用 LinkedHashMap 实现有序哈希表。

   public char firstUniqChar(String s) {
        Map<Character, Boolean> isExist = new LinkedHashMap<>();
        int len = s.length();
        for(int i = 0; i < len; ++i){
            isExist.put(s.charAt(i), !isExist.containsKey(s.charAt(i)));
        }
        for (Map.Entry<Character, Boolean> characterBooleanEntry : isExist.entrySet()) {
            if(characterBooleanEntry.getValue())
                return characterBooleanEntry.getKey();
        }
        return ' ';
    }

Day4

JZ51：逆序对数@归并排序

排序，就是在消除逆序对的过程。参考《算法》P170（2.2 归并排序），在此介绍一下。

首先是归并算法。

public class Merge
{
	private static Comparable[] aux; // 归并所需的辅助数组
	public static void sort(Comparable[] a){
		aux = new Comparable[a.length]; // 一次性分配空间
		sort(a, 0, a.length - 1);
	}
	private static void sort(Comparable[] a, int lo, int hi){
    	if (hi <= lo) return;
		int mid = lo + (hi - lo)/2;
		sort(a, lo, mid); // 将左半边排序
		sort(a, mid+1, hi); // 将右半边排序
		merge(a, lo, mid, hi); // 归并结果（代码见“原地归并的抽象方法”）
	}
    public static void merge(Comparable[] a, int lo, int mid, int hi){
		int i = lo, j = mid+1;
		for (int k = lo; k <= hi; k++) // 将a[lo..hi]复制到aux[lo..hi]
			aux[k] = a[k];
		for (int k = lo; k <= hi; k++){
			if (i > mid) a[k] = aux[j++];//左半边用尽（取右半边的元素）
			else if (j > hi ) a[k] = aux[i++];//右半边用尽（取左半边的元素）
			else if (less(aux[j], aux[i])) a[k] = aux[j++];//右半边当前元素小于左半边的当前元素（取右半边的元素）	
			else a[k] = aux[i++];//右半边的当前元素大于等于左半边的当前元素（取左半边的元素）
    	}
	}}

然后根据逆序对的性质，就是合成时的两个有序数组，左边比右边大的位置差，因此，对于逆序对，其全部产生于第三个判断，有：

if (tmp[j] < tmp[i]) {nums[k] = tmp[j++]; cnt+=mid-i+1;}

JZ52：链表公共节点

思路1：长度差 + 快慢指针。

思路2：注意到从后往前数比较简单，联想到一个很棒的数据结构——后进先出的栈。

通过栈思想，可以达到类似于逆序读入的效果。

 		Stack<ListNode> A = new Stack<ListNode>();
        Stack<ListNode> B = new Stack<ListNode>();
        ListNode tmp = headA;
        if(headA == null || headB == null)  return null;
        while (headA != null){
            A.push(headA);
            headA = headA.next;
        }
        while (headB != null){
            B.push(headB);
            headB = headB.next;
        }
        if(A.peek() != B.peek())    return null;
        while (!A.isEmpty() && !B.isEmpty() && A.peek() == B.peek()){
            A.pop();B.pop();
        }
        if(A.isEmpty() && B.isEmpty()) return tmp;
        if(A.isEmpty()) return B.peek().next;
        else return A.peek().next;

JZ53：有序数组频率查询

二分查找的变体。

JZ54：BST的第k大节点@逆中序遍历

方法1：中序遍历求[size-k]的值；

方法2：逆向中序遍历，得到第k个值

    int k, ans;
    public int kthLargest(TreeNode root, int k) {
        this.k = k;
        dfs(root);
        return ans;
    }
    private void dfs(TreeNode r){
        if(r == null) return;
        dfs(r.right);
        if(--k == 0)  {ans = r.val; return;}
        dfs(r.left);
    }

JZ55： 是否是AVL

我们提到过，已遍历节点为未遍历节点提供信息。所以本题选择后序遍历（自底向上）。

能否从左右子树的平衡因子，得到根的平衡因子呢？不可以哦。所以我们需要记录深度信息。

class Solution {
    public boolean isBalanced(TreeNode root) {
        return height(root) >= 0;
    }
    public int height(TreeNode root) {// -1 代表非平衡子树
        if (root == null)  return 0;
        int lh = height(root.left), rh = height(root.right);
        if (lh == -1 || rh == -1 || Math.abs(lh - rh) > 1) return -1;
        else     return Math.max(leftHeight, rightHeight) + 1;
    }
}

Day5

JZ56：数组中数字出现的次数@分组位运算

（1|2,2,2…）对于根据 x ^ x = 0, x ^ y != 0以及异或的结合性，先对全体元素异或，得到的是两个不同元素的数的异或结果。我们要找到最低位的“1”（或任意”1”，对应两个数位不同）进行分组，其掩码与元素们逐个异或判断，即可找到我们想要的数。

下面分析较为复杂的情况：除一个数字只出现一次外，其他数字均出现三次。找出独元素。

参：LeetCode题解Krahets

Picture4.png

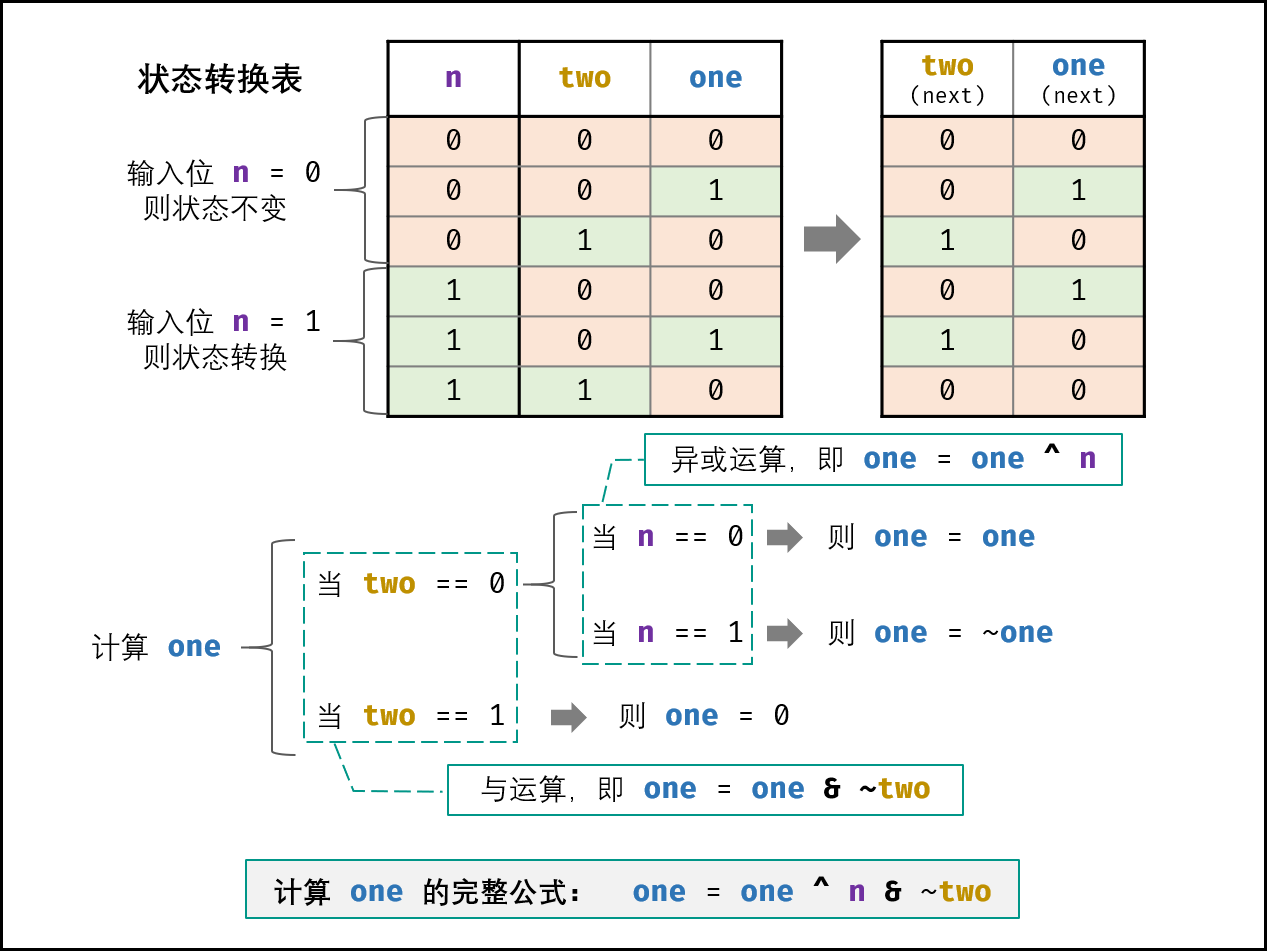
JZ57：和为s的连续正数序列

剑指 Offer 57 - II. 和为s的连续正数序列 - 力扣（LeetCode）

滑动窗口即可。当 s == target 和 s > target 时移动边界操作相同，因此可以合并。

    public int[][] findContinuousSequence(int target) {
        int i = 1, j = 2, sum = 3;
        List<int[]> res = new ArrayList<>();
        while(i < j) {
            if(sum == target) {
                int[] ans = new int[j - i + 1];
                for(int k = i; k <= j; k++)
                    ans[k - i] = k;//generate a list
                res.add(ans);
            }
            if(sum >= target) {
                sum -= i;		i++;
            } else {
                j++;	sum += j;
            }
        }
        return res.toArray(new int[0][]);
    }

Day 6

JZ60：n个骰子朝上点数和s概率@dp方向

显然，$dp[n][s] = \sum_1^6dp[n-1][s-i]\times\frac{1}{6}$

我们知道，每个阶段的状态都只和它前一阶段的状态有关，不需要用额外的一维来保存所有阶段。

我们注意到s - i可能会为负数，这里可以考虑换一个状态转移方向：

			for (int j = 0; j < cursum; j++) {
                for (int i = 0; i < 6; i++) {
                    tmp[j + i] += dp[j] / 6.0;
                }
            }

JZ61：扑克牌中的顺子（王视为Any）

遍历五张牌，满足max - min <= 5。遇到大小王（即 0 ）直接跳过。

		Set<Integer> repeat = new HashSet<>();
        int max = 0, min = 14;
        for(int num : nums) {
            if(num == 0) continue; 
            max = Math.max(max, num); min = Math.min(min, num);
            if(repeat.contains(num)) return false; 
            repeat.add(num); // 添加此牌
        }
        return max - min < 5;

数字电路系列

用位运算实现加法器等…理解下：程序是个状态机。提示：CSAPP介绍过，位级别一致性。

Day7

JZ66：构建乘积数组

from：Krahets(https://leetcode-cn.com/u/jyd/)

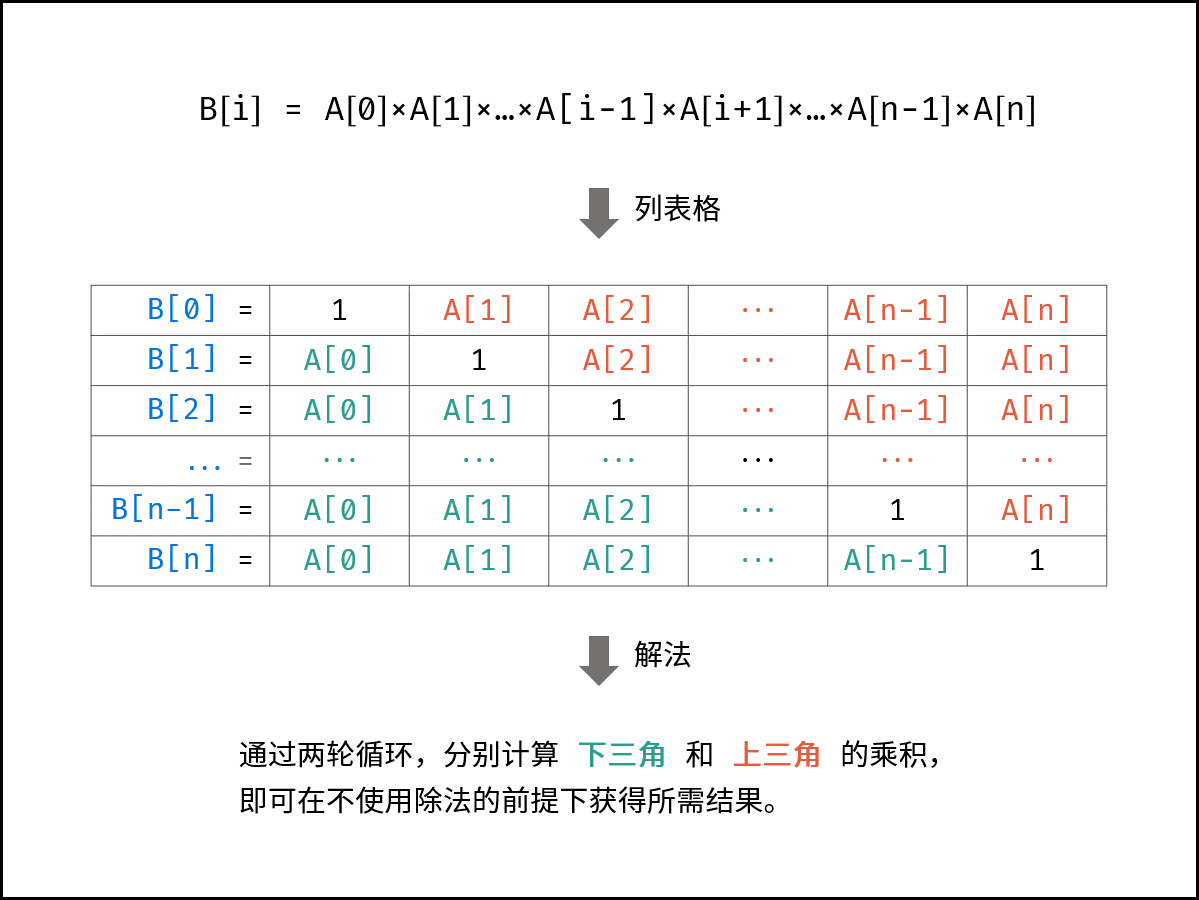
JZ68：二叉树的公共祖先

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == nullptr || root == p || root == q) return root;
        TreeNode *left = lowestCommonAncestor(root->left, p, q);
        TreeNode *right = lowestCommonAncestor(root->right, p, q);
        if(left == nullptr) return right;
        if(right == nullptr) return left;
        return root;
}

上述代码通过递归实现了“自底向上”的效果。在返回时，体现了路径的回溯。

接下来还有一种思路，是中序遍历。根据中序遍历的顺序，遍历的顺序一定是（含同时）：左节点->公共祖先->右结点。循环时，如果找到其中一个指定节点，其本身作为祖先作为res记录并维护。记录res的当前高度为deep，继续遍历此后的节点，在其下方者均以res为祖先，如果遍历时遇到节点的深度浅于当前记录（向上）则更新，直到遇到第二个指定节点。

TreeNode* lowestCommonAncestor(TreeNode* root,TreeNode* p,TreeNode* q) {
        stack<TreeNode*> st;
        TreeNode * res;
        int deep = 0;//记录**当前结果祖先结点**的深度
        while (root || !st.empty()) {
            while (root) {
                st.push(root);
                root = root->left;
            }
            TreeNode *t = st.top();
            if (st.size() < deep) {//一定是找到一个结点之后且向上才有可能满足
                deep = st.size();//可以理解为，st.size()就是t的深度
                res = t;//说明较深处祖先下方无第二个结点，故更新结果为上一层祖先
            }//需要在判等前处理，否则恰好新祖先就是第二个结点则比对错误
            if (t == p || t == q) {//该语句块会先后以两个条件执行两次
                if (deep == 0) {//根 || 首次进入这里
                    deep = st.size();
                    res = t;
                }
                else
                    return res;
            }
            st.pop();
            root = t->right;
        }
        return nullptr;
     }

将有向无环图中的顶点 v 的高度定义为从根结点到 v 的最长路径。在所有 v 和 w 的共同祖先中，高度最大者就是 v 和 w 的最近共同祖先。LCA 的计算在实现编程语言的多重继承中很有用。参考：http://www.ics.uci.edu/~eppstein/261/BenFar-LCA-00.pdf