数据结构补充知识

线段树

线段树是常用的用来维护 区间信息 的数据结构，可以在O(log)的时间复杂度内实现单点修改、区间修改、区间查询（区间求和，求区间最大值，求区间最小值）等操作。

线段树是一颗近似的完全二叉树，每个节点代表一个区间，节点的权值是该区间的一个属性。也可以理解成：树状数组。

实例：求区间[l, r]的总和。数组：{10, 11, 12, 13, 14}

我们就可以得到类似于这样的线段树：

void build(int s, int t, int p) { // 对 [s,t] 区间建立线段树,当前根的编号为 p
	if (s == t) { d[p] = nums[s]; return; }//根节点管辖的区间长度为1,直接赋值
	int mid = s + ((t - s) >> 1);
	build(s, mid, p * 2), build(mid + 1, t, p * 2 + 1); 
	// 自底向上递归，左右区间建树 
	d[p] = d[p * 2] + d[(p * 2) + 1]; 
}

如此，对于区间的查询和数据更新，能够通过迭代，达到比较优秀的性能。

通过非叶子节点的“懒惰标记”，表示该节点所有对应的孩子节点都应该有此更新，延迟对节点信息的更改，从而减少可能不必要的操作次数。

// 区间修改 - 增加值
void update(int l, int r, int c, int s, int t, int p) { // [l, r] 为修改区间, c 为被修改的元素的变化量, [s, t] 为当前节点包含的区间, 为当前节点的编号 
	if (l <= s && t <= r) { d[p] += (t - s + 1) * c, b[p] += c; return; } 
	// 当前区间为修改区间的子集时直接修改当前节点的值,然后打标记,结束修改 
	int m = s + ((t - s) >> 1); 
	if (b[p] && s != t) { // 如果当前节点的懒标记非空,则更新当前节点两个子节点的值和懒标记值 
	d[p * 2] += b[p] * (m - s + 1), d[p * 2 + 1] += b[p] * (t - m); 
	b[p * 2] += b[p], b[p * 2 + 1] += b[p]; // 将标记下传给子节点
	b[p] = 0; // 清空当前节点的标记 
	} 
	if (l <= m) update(l, r, c, s, m, p * 2); 
	if (r > m) update(l, r, c, m + 1, t, p * 2 + 1); 
	d[p] = d[p * 2] + d[p * 2 + 1]; 
}

参考：树状数组 - OI Wiki (oi-wiki.org) 线段树 - OI Wiki (oi-wiki.org)

如果你已经对线段树足够熟悉了，可以练习307. 区域和检索（视频讲解)

二维前缀和/积分图

前缀和的一个应用是概率平均，TODO

304. 二维区域和检索 - 矩阵不可变

数学基础： fig1

代码实现如下：

// TO get DP
    sum.resize(n+1, vector<int>(m+1,0));// 注意预处理！
    for(int i = 1; i <= n; i++) 
        for(int j = 1; j <= m; j++)
            sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + matrix[i-1][j-1];

//TO get a[x1:x2][y1:y2]
    x1++; y1++; x2++; y2++;
    ans = sum[x2][y2] - sum[x1-1][y2] - sum[x2][y1-1] + sum[x1-1][y1-1];

可参考：前缀和 & 差分 - OI Wiki

学习完前缀和后，可以练习560. 和为 K 的子数组

动态开点线段树

对于一些值域比较大的查询，使用4 * n 容量可能导致浪费。对于稀疏信息比较友好的“动态开点”策略线段树或许是个更好的选择。模板：

/**
 * @Description: 线段树（动态开点）
 * @Author: LFool
 * @Date 2022/6/7 09:15
 **/
public class SegmentTreeDynamic {
    class Node {
    //结点本身是不需要存储l, r的，这个是函数参数获得的。对应下方相关函数的[start, end]
        Node left, right;
        int val, add;
    }
    private int N = (int) 1e9;
    private Node root = new Node();
    // 当前树结点的区间为 [start, end] ，需要更新区间 [l, r] 的值，将区间 [l, r]中的所有元素均 + val
    public void update(Node node, int start, int end, int l, int r, int val) {
        if (l <= start && end <= r) {
            node.val += (end - start + 1) * val;
            node.add += val;
            return ;
        }
        int mid = (start + end) >> 1;
        pushDown(node, mid - start + 1, end - mid);
        if (l <= mid) update(node.left, start, mid, l, r, val);
        if (r > mid) update(node.right, mid + 1, end, l, r, val);
        pushUp(node);
    }
    public int query(Node node, int start, int end, int l, int r) {
        if (l <= start && end <= r) return node.val;
        int mid = (start + end) >> 1, ans = 0;
        pushDown(node, mid - start + 1, end - mid);
        if (l <= mid) ans += query(node.left, start, mid, l, r);
        if (r > mid) ans += query(node.right, mid + 1, end, l, r);
        return ans;
    }
    private void pushUp(Node node) {
        node.val = node.left.val + node.right.val;
    }
    //懒惰标记下推，左右分别是子节点区间长度，用于初始化结点的值。
    private void pushDown(Node node, int leftNum, int rightNum) {
        if (node.left == null) node.left = new Node();
        if (node.right == null) node.right = new Node();
        if (node.add == 0) return ;
        node.left.val += node.add * leftNum;
        node.right.val += node.add * rightNum;
        // 对区间进行「加减」的更新操作，下推懒惰标记时需要累加起来，不能直接覆盖
        node.left.add += node.add;
        node.right.add += node.add;
        node.add = 0;
    }
}

区间最值系列

【TBD】

单调栈/单调队列

单调栈 - OI Wiki

将一个元素插入单调栈时，为了维护栈的单调性，需要在保证将该元素插入到栈顶后整个栈满足单调性的前提下弹出元素。这个弹出的元素，是最新的破坏单调性质的元素。或者说，栈是个暂存区。

其实只需要填空实现：我们发现了，只要是遇到了相邻两点单调递（）破坏了单调性质，根据当前栈顶和当前遍历的元素值 更新答案。

跳表

跳表是对有序链表的改进。跳表的期望空间复杂度为O(n) ，跳表的查询，插入和删除操作，期望时间复杂度都为 O(logn)

每层以一定的概率筛选出向上一层的元素。
查找时则从顶层开始找。
增删则通过伪随机数控制高度。

如果是面试使用的模板，这里的每个节点并不是每层都有一个Node，可以是公用的，带上vector字段对应每一层。

1206. 设计跳表 - 力扣（LeetCode）

获取节点的最大层数

模拟以$p$的概率往上加一层，最后和上限值取最小。

int randomLevel() {
  int lv = 1;
  // MAXL = 32, S = 0xFFFF, PS = S * P, P = 1 / 4
  while ((rand() & S) < PS) ++lv;
  return min(MAXL, lv);
}

查询

查询跳表中是否存在键值为 key 的节点。具体实现时，可以设置两个哨兵节点以减少边界条件的讨论。

V& find(const K& key) {
  SkipListNode<K, V>* p = head;

  // 找到该层最后一个键值小于 key 的节点，然后走向下一层
  for (int i = level; i >= 0; --i) {
    while (p->forward[i]->key < key) {
      p = p->forward[i];
    }
  }
  // 现在是小于，所以还需要再往后走一步
  p = p->forward[0];

  // 成功找到节点
  if (p->key == key) return p->value;

  // 节点不存在，返回 INVALID
  return tail->value;
}

插入

插入节点 (key, value)。插入节点的过程就是先执行一遍查询的过程，中途记录新节点是要插入哪一些节点的后面，最后再执行插入。每一层最后一个键值小于 key 的节点，就是需要进行修改的节点。

void insert(const K &key, const V &value) {
  // 用于记录需要修改的节点
  SkipListNode<K, V> *update[MAXL + 1];

  SkipListNode<K, V> *p = head;
  for (int i = level; i >= 0; --i) {
    while (p->forward[i]->key < key) {
      p = p->forward[i];
    }
    // 第 i 层需要修改的节点为 p
    update[i] = p;
  }
  p = p->forward[0];

  // 若已存在则修改
  if (p->key == key) {
    p->value = value;
    return;
  }

  // 获取新节点的最大层数
  int lv = randomLevel();
  if (lv > level) {
    lv = ++level;
    update[lv] = head;
  }

  // 新建节点
  SkipListNode<K, V> *newNode = new SkipListNode<K, V>(key, value, lv);
  // 在第 0~lv 层插入新节点
  for (int i = lv; i >= 0; --i) {
    p = update[i];
    newNode->forward[i] = p->forward[i];
    p->forward[i] = newNode;
  }

  ++length;
}

删除

删除键值为 key 的节点。删除节点的过程就是先执行一遍查询的过程，中途记录要删的节点是在哪一些节点的后面，最后再执行删除。每一层最后一个键值小于 key 的节点，就是需要进行修改的节点。

bool erase(const K &key) {
  // 用于记录需要修改的节点
  SkipListNode<K, V> *update[MAXL + 1];

  SkipListNode<K, V> *p = head;
  for (int i = level; i >= 0; --i) {
    while (p->forward[i]->key < key) {
      p = p->forward[i];
    }
    // 第 i 层需要修改的节点为 p
    update[i] = p;
  }
  p = p->forward[0];

  // 节点不存在
  if (p->key != key) return false;

  // 从最底层开始删除
  for (int i = 0; i <= level; ++i) {
    // 如果这层没有 p 删除就完成了
    if (update[i]->forward[i] != p) {
      break;
    }
    // 断开 p 的连接
    update[i]->forward[i] = p->forward[i];
  }

  // 回收空间
  delete p;

  // 删除节点可能导致最大层数减少
  while (level > 0 && head->forward[level] == tail) --level;

  // 跳表长度
  --length;
  return true;
}

动态规划专题

Welcome😀Dynamic Programming Patterns

背包问题

2. 01背包问题 - AcWing题库 3. 完全背包问题 - AcWing题库

遍历的顺序：根据状态转移方程的依赖箭头同向，范围肯定是从子问题开始

==总结== 0 - 1背包对物品的迭代放在外层，里层的体积或价值逆向遍历；完全背包对物品的迭代放在里层，外层的体积或价值正向遍历。

对于背包问题，dp[i][j] 表示只能放前 i 个物品的情况下，容量为j的背包可达到的价值总和最大值。

状态压缩时要注意什么？注意被压缩的那个维度！注意遍历顺序，获取正确的转移前状态。

求方案数：278. 数字组合 - AcWing题库

树状DP

树形 DP，即在树上进行的 DP。由于树固有的递归性质，树形 DP 一般都是递归进行的。(其实本质是后序遍历 )可以通过 DFS，在返回上一层时更新当前结点的最优解。

P2014 [CTSC1997] 选课 - 洛谷 337. 打家劫舍 III - 力扣（LeetCode）：可以考虑哈希映射、函数返回状态进行记忆化

状压DP

对于从数组中选取子集[pick, unpick, pick...]可以使用整数的二进制位进行表示（一般此类题的数组长度上限很小）。此时，可用相应的整数表示子集，子集可以作为状态转移方程的维度，整数的加减表示状态之间的转移。

哈希

哈希表的查询时间复杂度是O(1)

HashCode

数组下标的计算方法是 (n - 1) & hash。（n 代表数组长度）且HashMap 的长度是 2 的幂次。

这个算法应该如何设计的？

取余(%)操作中如果除数是 2 的幂次则等价于与其除数减一的与(&)操作，采用二进制位操作 &，相对于%能够提高运算效率。

哈希示例

值得提醒的是有哈希并不显式地展示哈希表。如442. [1, n]数组中重复的数据，即就地哈希思想。Leetcode-offer1#JZ35：复制盲盒链表@就地哈希中也是使用了链表原地复制 的就地方式。

字符串专题

字典树

参考：《算法4》· 单词查找树，dsacpp习题9-26

示例

实现

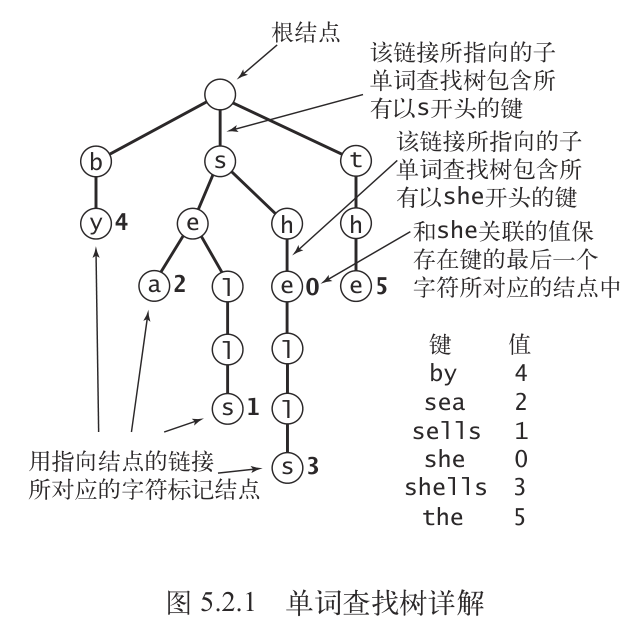
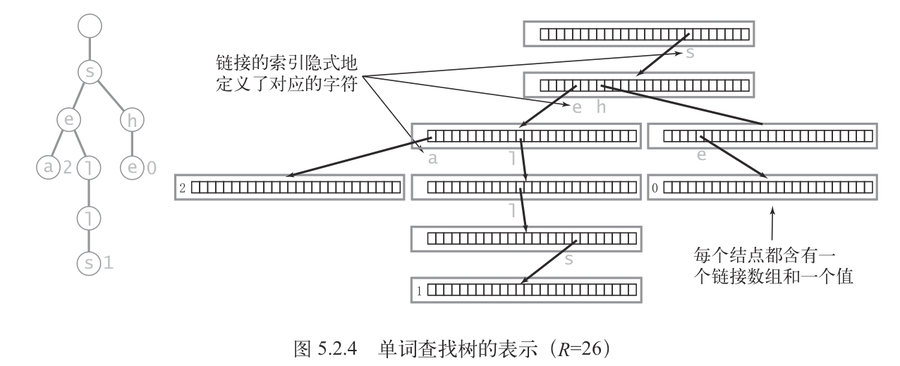
该数据结构具有以下特性：

这里结点对应的编号是字符串键对应的结束状态。
每个结点都含有字符集长度个指针数组
值为空的结点在符号表中没有对应的键，它们的存在是为了简化单词查找树中的查找操作。

欢迎尝试实现

KMP算法

KMP是字符串匹配算法。其思路是：最大限度地利用此前匹配所提供的信息，尽可能大跨度地右移模式串。

匹配过程如下：

查之前已经匹配成功的部分中里是否存在「前缀」==「后缀」的部分。如果存在，则跳转到「前缀」的下一个位置继续往下匹配。
如果此时字符不匹配，从起始位置继续开始。

于是我们引出next数组，以记录原串的性质：最长公共前后缀的长度。(约定：最长前缀不包含最后一个字符)。于是，就可以把新一轮匹配放在next[i]开始了。

进一步优化之，利用“匹配失败”带来的信息，在中断的位置，

vector<int> buildNext(string P) {
    int len = P.size();
    vector<int> next(len);
    int t = next[0] = -1;
    int j = 0;
    while (j < len - 1) {
        if (t < 0 || P[j] == P[t]) {
            t++;
            j++;
            next[j] = (P[j] != P[t] ? t : next[t]);  //充分优化
        } else                                       //失配
            t = next[t];
    }
    return next;
}

int strStr(string haystack, string needle) {
    vector<int> next = buildNext(needle);
    int slen = haystack.size(), plen = needle.size();
    for (int i : next) {
        cout << i << " ";
    }
    int i = 0, j = 0;
    while (i < slen && j < plen) {
        if (j < 0 || haystack[i] == needle[j]) {
            i++;
            j++;
        } else {
            j = next[j];
        }
    }
    if (j == plen)
        return i - j;
    return -1;
}

AC自动机

TODO

树

Morris遍历

大体流程：

记当前节点的指针为 cur。
如果 cur 所指向的节点没有左孩子，那么 cur 指针向右移动。
如果 cur 所指向的节点有左孩子， mostright 指针指向该 cur 左子树的最右节点。
- 如果 mostright 所指向的节点的 right 指针为空，那么让mostright 的 right 指针指向 cur，然后cur 指针向左移动；
- 如果 mostright 所指向的节点的 right 指向 cur，那么让 right 重新指向空，然后 cur 向右移动。

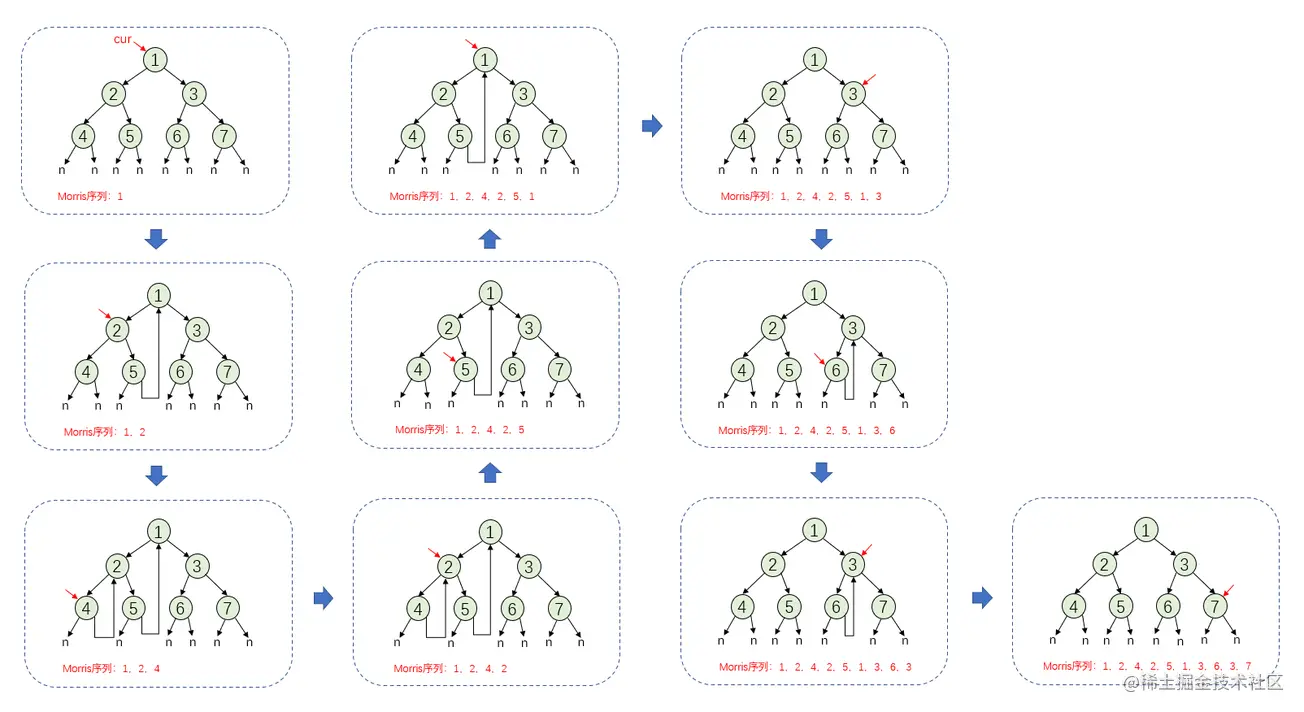
根据访问节点的顺序，判断指针行为，找到三次遍历时对应的处理时机。

图论经典算法

Prim

延迟：每当我们向树中添加了一条边之后，也向树中添加了一个顶点。要维护一个包含所有横切边的集合，就要将连接这个顶点和其他所有不在树中的顶点的边加入优先队列 。每次取优先队列中权重最小的且有效的（懒惰，判断边的两个顶点都在树中，则排除）。

即时：我们不需要在优先队列中保存所有从 w 到树顶点的边——而只需要保存其中权重最小的那条，在将 v 添加到树中后检查是否需要更新这条权重最小的边。维护每个节点的最小距离（多个堆）即连接w和树的最佳边Edge。

Kruskal

按照边的权重顺序（从小到大），将边加入最小生成树中，并保持加入的边不会与已经加入的边构成环，直到树中含有 V-1 条边为止。这些边逐渐由一片森林合并为一棵树，也就是图的最小生成树。其中，判断加入此边是否成环，可以使用并查集。

排序

【自主命题】给定一个元素不重复的数组，进行升序排序，你需要返回排序后下标之间的对应关系，你可以自由地设计返回的形式。请看例子：输入数组[5, 8, 7, 9]，你可以：

返回所有逆序对（索引 / 元素）：{1, 2}
返回新的下标对应关系：[0, 2, 1, 3]
返回元素与下标的map：{5, 0}, {8, 2}, {7, 1}, {9, 3}。不变者也可以不在返回结果中。期望在$O(logn)$的时间复杂度下得到结果。

最后更新于2年前

这有帮助吗？