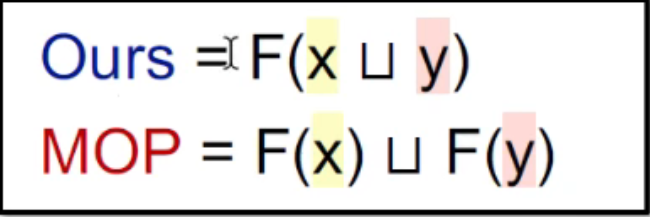静态软件分析-执行流

Intro

  • More focus on soundness (false negatives)

  • over-approximated static analysis produces false positives

Intermediate Representation

3-address form

  • control flow visible

  • compact and uniform

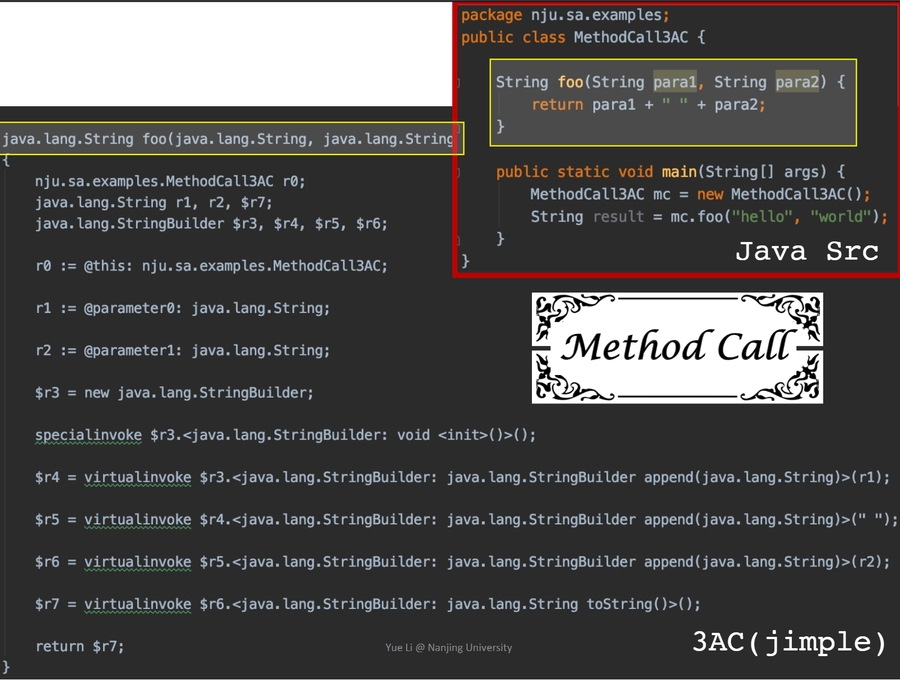
eg: Java soot Method Call demo:

Static Simple Assignment(SSA)

给每一个definition都分配一个新的“变量”来用。 优点：弱化控制流的强表示。 缺点：转换成机器码存在问题。

Control Flow Analysis

CFG nodes：Basic Blocks

BB：max instruction set that can be entered only at the first instruction, as out only at last

Data Flow Analysis - AP

Preliminaries

  • 状态机转换：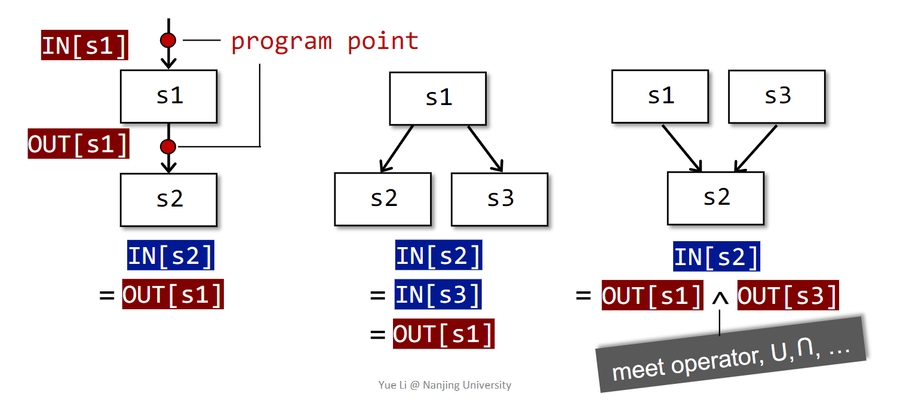

  • 形式化描述：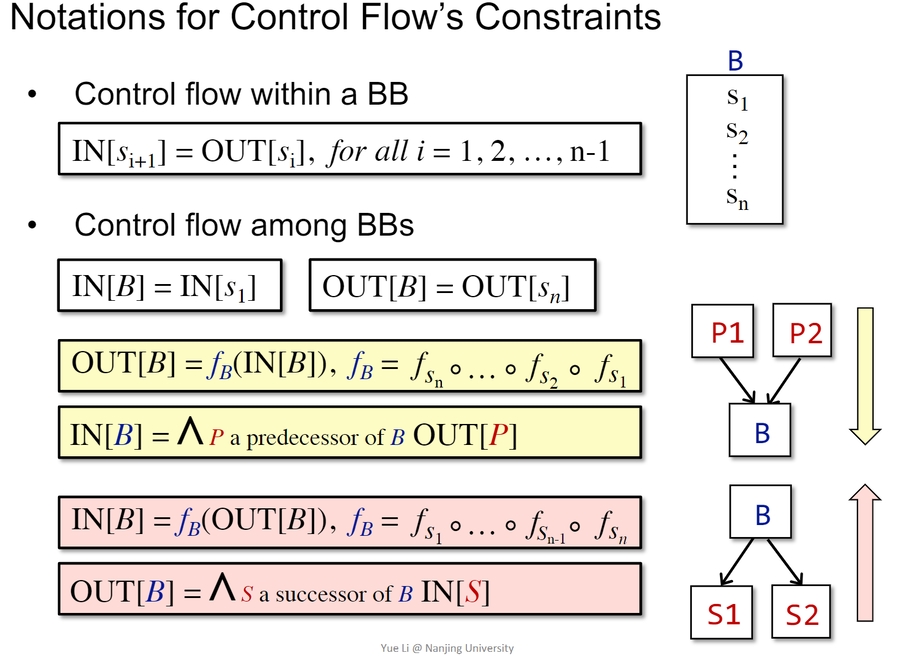

  • 基本转换函数 OUT(B)=genB∪(IN(B)−killb)OUT(B) = gen_B \cup (IN(B)-kill_b)

Reaching Definition Analysis

此算法的灵魂在于：IN[B]不变，则OUT[B]不变。（其他是常量） 此算法的有穷性表现为：IN的变化表示为“更多的流入信息”，信息流在静态程序中是有限的，因此OUT为单增的（只会set 1）。 从循环不变式的角度来说，由于IN完全依赖于OUT，因此终止条件是安全的不动点。

Live Variable Analysis

-> 此次定义未被use，则不必存入寄存器（v is dead at p）

used: before redefinition in B， eg x = x - 1 为什么用backward? 其实forward也可以，不过更好传递usage和define的消息带到前面去判断，减少迭代次数。(这里OUT不变，IN不变，与上一个算法的依赖相反，是巧合吗？)

Available Expressions Analysis

指在程序点上，哪个表达式在所有到达此处的路径上已经被计算过了且没有修改。如果被计算，那么可以复用原值。if：

  • all paths from the entry to p must pass through the evaluation of x op y

  • after the last evaluation of x op y, there is no redefinition(kill) of x or y 这是一个must analysis(under-approximation, safe)。 | 优化前 | 优化后（使用last evaluation） | | ---------------------------------------------------------- | ------ | | | |

  • 先看kill

  • 作为must analysis，初始化的值为全1.

  • forward

Analysis Comparison

Data Flow Analysis - FD

不动点定理

不动点：$f(V)=V$

complete lattice: any subset $S$ of $P$ has LUB and GLB

Relate Iterative Algorithm to Fixed Point Theorem

  • 转移函数是单调的。

  • 根据格的定义，Join/Meet是单调的。

  • 算法迭代，经过的node迭代不会超过height of lattice

  • JOIN作为LUB，因此可以达到Control Flow的最符合预期的不动点。(minimal step)

May/Must Analysis, A Lattice View

Meet-Over-all-Paths（MOP）

图
解释

每条path对应$F_p$操作的结果进行Meet或者Join。 有些path在软件跑起来时不会走这条路（executable） 很难在大程序中进行枚举（Unbounded） （$MOP\sqsubseteq OURS$OURS->Iterative Algo.)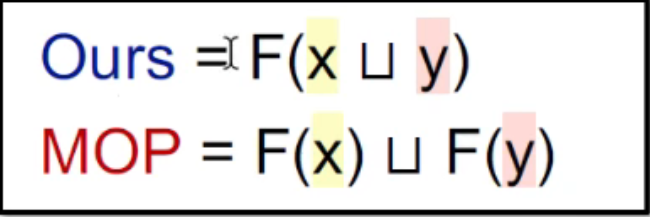

Constant Propogation

为了保证单调性，UNDEF作为更bottom的node。（const + undef = undef）因此，不再满足可分配性。

WorkList Algorithm

A1: 活跃变量分析和迭代求解器

实验前提示，IDEA在A1/tai-e目录下打开项目比较好用。注意JDK不要选错哦~

LValue & RValue

在 Tai-e 的 IR 中，我们把表达式分为两类：LValue 和 RValue。前者表示赋值语句左侧的表达式，如变量（x = … ）、字段访问（x.f = …）或数组访问（x[i] = …）；后者对应地表示赋值语句右侧的表达式，如数值字面量（… = 1;）或二元表达式（… = a + b;）。而有些表达式既可用于左值，也可用于右值，就比如变量（用Var类表示)。

在C++中的理解：左值（lvalue）是一个表达式，它表示一个可被标识的（变量或对象的）内存位置，并且允许使用&操作符来获取这块内存的地址。如果一个左值同时是引用，就称为“左值引用”。

  • Java的变量模型和传统C++不一样。如果你想复制一个对象，你可能需要new一个新的，再把它set成对应的内容。

对于声明的类型转换，依赖关系的验证的方式是 sub instanceof sup

也是因此，上面的类间关系图显得比较灵活可用。弄清楚函数之间调用的输入输出（签名），方可更好地理解信息如何在程序中传递。

注意：transferNode函数是有返回值的，在以后的实验中也可以利用好这点。注意不要T/F搞混哦。

另外，老生常谈了，如果你没有思路，请看看手册里是不是还有没用上的内容。

【在LiveVariableAnalysis中你获得的道具】

  • Maybe.. None

A2：常量传播和 Worklist 求解器

很容易发现，Exp类是非常核心的一个类。（翻译：表达式包含变量、字面量、二元表达式三种，你需要在某个地方判断是哪种或者需要分类讨论）我们不妨先复习几个概念：

  • IR是SPA的处理对象。这些对象间的执行流就是CFG。

  • IR中的Stmt对应语句，可以获取左值、右值等。

  • IR 中的一个关键接口Exp，表示各种表达式。

  • 按照Java规范，可以把常量称作字面量（Literals）。每个 IntLiteral 类的实例都表示一个程序中的整数字面量。你可以通过调用 getValue() 方法来获取它的值。

实现细节

  • 表达式求值，想到了什么？递归。

  • 在这里回顾一些细节：

    1. 不要忘了在 Solver.initializeForward() 中初始化每个语句的 IN 和 OUT，给予一样的初值。这样是为了实现对应的 meet 策略，使得每次合并两个集合不会创建出一个新的对象保存结果。TODO，这种设计还有更多的优化空间：我们可以忽略一些不变的 IN fact 来提高效率。

    2. 你需要清楚地知道你的代码在做些什么。比如： 对于除以 0 的情况（出现在 / 和 % 中），我们规定结果为 UNDEF。例如，对于 x = a / 0，就算a 是NAC，x 的值也将会是 UNDEF。为什么呢？

道具：表达式求值

  • Value evaluate(Exp,CPFact) ConstantPropagation.evaluate方法会计算表达式（Exp）的值（Value）。当然，此处的值是格上的抽象值。

A3：死代码检测

实现设计

  • 我这里使用了两个模式。liveStmt和deadCode，对应降低复杂度。争取每一个code遍历时都能找到 自己的归宿。最终：code - liveStmt 放入 deadCode（sound？）

  • 对于switch，要比较小心。比如说：fallthrough到default。

  • 实际上，fallthrough已经在CFG实现，而不是通过canFallthrough方法判断的，我这里的处理方式是将其他的分支直接出队，而不是重复遍历。 因为生成的IR图是这样的，所以你不必按类似于查找表的方式处理它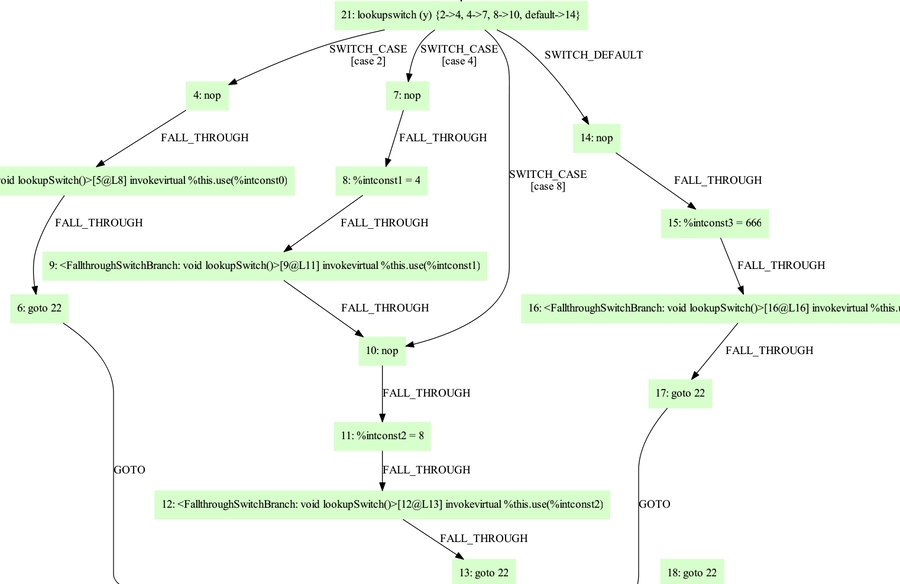

道具：右值副作用

DeadCodeDetection.hasNoSideEffect(RValue)，用来帮助你检查一个表达式是否含有副作用。

上一页软件工程下一页静态软件分析-上下文敏感

最后更新于

这有帮助吗？